Where to find Puzzle 117?
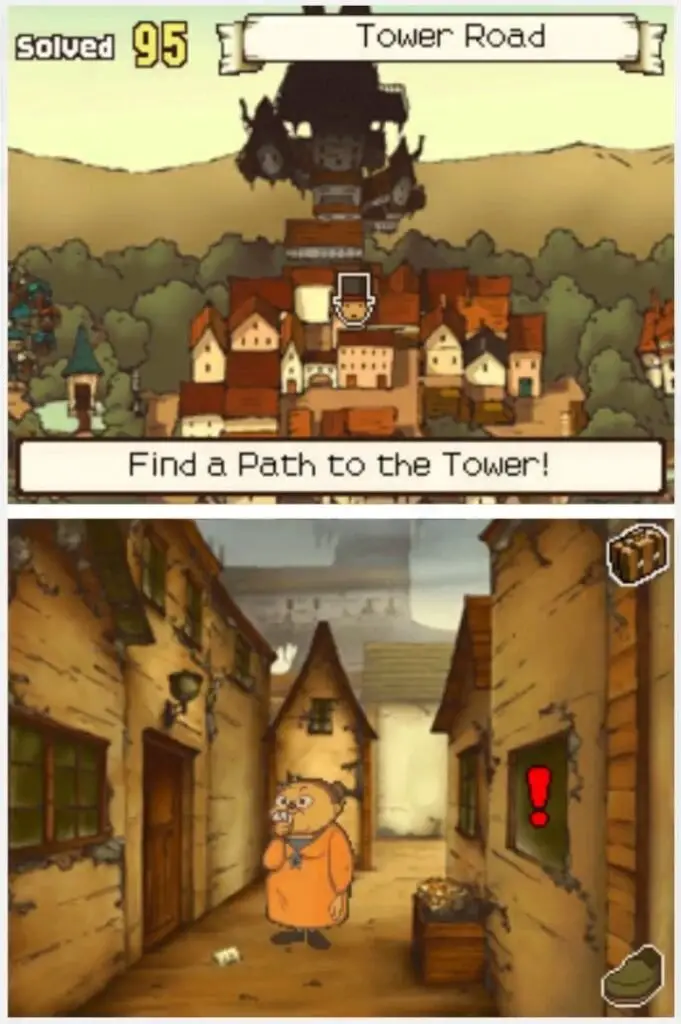
Puzzle 117 – Painting a Cube is found by interacting with the open window on the right side of Tower Road
How many picarats is Puzzle 117 worth?
Puzzle 117 is worth 30 picarats.
How to solve Puzzle 117?
For Puzzle 117, you need to figure out the maximum amount of different ways you can paint a cube using three colors of paint.

In front of you sits a blank paper cube that you’ve decided to paint. You need to paint the cube so that all faces that touch are different colors.
Using three colors of paint, how many ways can you paint the cube so that it satisfies the above condition?
Each painting scheme should be a different pattern, not just the same pattern with the colors rearranged. Also, assume that you can’t leave any sides of the square blank.
What are the hints for Puzzle 117?
Hint 1

As you know, all cubes have six sides. Because of this structure, every face of the cube touches four others, meaning that only one of the five other faces doesn’t touch any given face.
Hint 2

Taking Hint One a step further, in order to paint the cube three colors and have no two connecting faces be of the same color, you should use each color to paint opposing faces.
Hint 3

You need to paint two opposing faces of the cube each color. Count how many different ways there are of doing that and you’ve solved the puzzle.
Just remember, simply reconfiguring which colors go where doesn’t count as an entirely new arrangement.
Puzzle 117 Answer
You can only configure the cube 1 way.

How did you find this guide? Let me know in the comments.
Where to find Puzzle 117?

Puzzle 117 – Painting a Cube is found by interacting with the open window on the right side of Tower Road
How many picarats is Puzzle 117 worth?
Puzzle 117 is worth 30 picarats.
How to solve Puzzle 117?
For Puzzle 117, you need to figure out the maximum amount of different ways you can paint a cube using three colors of paint.

In front of you sits a blank paper cube that you’ve decided to paint. You need to paint the cube so that all faces that touch are different colours.
Using three colours of paint, how many ways can you paint the cube so that it satisfies the above condition?
Each painting scheme should be a different pattern, not just the same pattern with the colours rearranged. Also, you can’t leave any sides of the cube blank.
What are the hints for Puzzle 117?
Hint 1

As you know, all cubes have six sides. Because of this structure, every face of the cube touches four others, meaning that only one of the five other faces doesn’t touch any given face.
Hint 2

Taking Hint 1 a step further, in order to paint the cube three colours and have no two connecting faces be of the same colour, you should use each colour to paint opposing faces.
Hint 3

You need to use each colour to paint two opposing faces of the cube. Count how many different ways there are of doing that and you’ve solved the puzzle.
Just remember, simply reconfiguring which colours go where doesn’t count as an entirely new arrangement.
Puzzle 117 Answer
You can only configure the cube 1 way.

How did you find this guide? Let me know in the comments.



